Universal-Adversarial-Perturbations-Pytorch
Implementation of Universal Adversarial Perturbations paper for the CS-E4070 - Special Course in Machine Learning and Data Science: Advanced Topics in Deep Learning course at Aalto University, Finland.
The dataset used was the Fashion Mnist for simplicity and to be trainable on the cpu.
Paper interpretation
Adversarial examples are a big issue of machine learning models, especially neural networks. In this paper, the authors try to exploit some characteristics of this problem and the properties of the adversarial examples.
The paper has shown some impressive results:
-
It has shown that the state of the art neural networks can be fooled with a high probability on most of the images with the same computed adversarial example.
-
The paper also proposed the pseudo code of the algorithm implemented in this repository to find the perturbations that can fool with high probability most of the images shown to a neural network.
-
It is also shown and possible to see in this implementation that a rather small number of training samples is enough to generate a perturbation capable of fooling the network with high probability on the remaining data.
-
Although this part is not compared with the code in this repository, it is shown that these perturbations are somewhat capable to generalize also to other architectures. This is what the authors call “Doubly universal”, with respect to the data and to the architecture of the network.
-
Finally, it is shown that there is a geometric correlation behind these examples that make neural networks highly vulnerable if anyone with malicious intent tries to affect the system.
Other interesting topics on this paper:
-
This implementation doesn’t try to find a data point specific perturbation as previous algorithms do. Instead, it tries to find a perturbation that generalizes well to most data points.
-
The perturbations are based on some data distribution and not directly intended to be generalized across different models.
Universal Perturbations
The main goal is to find a perturbation where:
for most
The above formula can be translated to a perturbation v that when added to x, changes the output of K’ for most of the data points x drawn from the distribution.
The generated perturbation ‘v’ is subject to some constraints:
The first constraint is responsible to manage and regulate how small is the vector v. The second one ensures that the fooling rate for all images is above the defined threshold. On this implementation, the fooling rate is calculated using all the images on the test set.
Algorithm
The algorithm is simple and intuitive. It has a main loop that will keep running until the fooling rate constraint is satisfied. Inside this loop, there is an iteration across all data points. If the network is fooled by the current perturbation on the current data point there is no need to do anything more with it, and we move to the next data point. On the other hand, if the neural network is not fooled on that data point it is necessary to update the perturbation. To update the perturbation, and iteration of the DeepFool Algorithm is run as suggested on the paper, and the calculated perturbation is added to the current one, with the result being projected and resulting on the new perturbation.
The calculus to find the fooling rate is simply the division of the count of fooled images by the total number of images considered.
Due to the nature of this algorithm, it is not guaranteed that the found perturbation is the best perturbation, or even that it is unique. The constraints are quite broad and allow a significant variance on the perturbations find on multiple runs of the algorithm. Therefore, this is not an algorithm to find the smallest universal perturbation. It is mentioned in the paper that the algorithm can be manipulated and changed to find multiple adversarial universal perturbations that satisfy all the constraints.
Vulnerability to Universal Perturbations
After some comparisons, the authors found that the gap on the fooling rate of the universal perturbations and random perturbations is motivated by the exploration of geometric properties of the data points. They even say that if the data used was completely uncorrelated, results from the random and universal perturbations would be comparable.
The authors theorize about the existence of subspaces that collect normal vectors to the decision boundary. These vectors are a key element responsible for this vulnerability since the gap between other algorithms and this one can be explained by the fact that this one does not select random vectors in those subspaces, it finds the one that maximizes the fooling rate across data points.
Future work and considerations
Although this paper explores the vulnerability present on neural networks related to adversarial examples, pushing it even further with the help of universal perturbations that do not need to be crafted specifically for each example, it is not able to present a decent solution to this problem.
Even after trying to use the generated perturbations to fine-tune the model with adversarial training, it did not yield any impressive or significative result.
As future work, it is important to better understand the geometric correlation between data points and the connection with the fooling rate, as well as, coming up with alternative training techniques to overcome those vulnerabilities and reduce their impact at least. One possibility is to use this geometric correlation on the training process.
Finally, the paper has shown that models are still exposed to high risks and can possibly be fooled by malicious individuals.
Running the project
The project is runnable from the main file.
Implementation Results
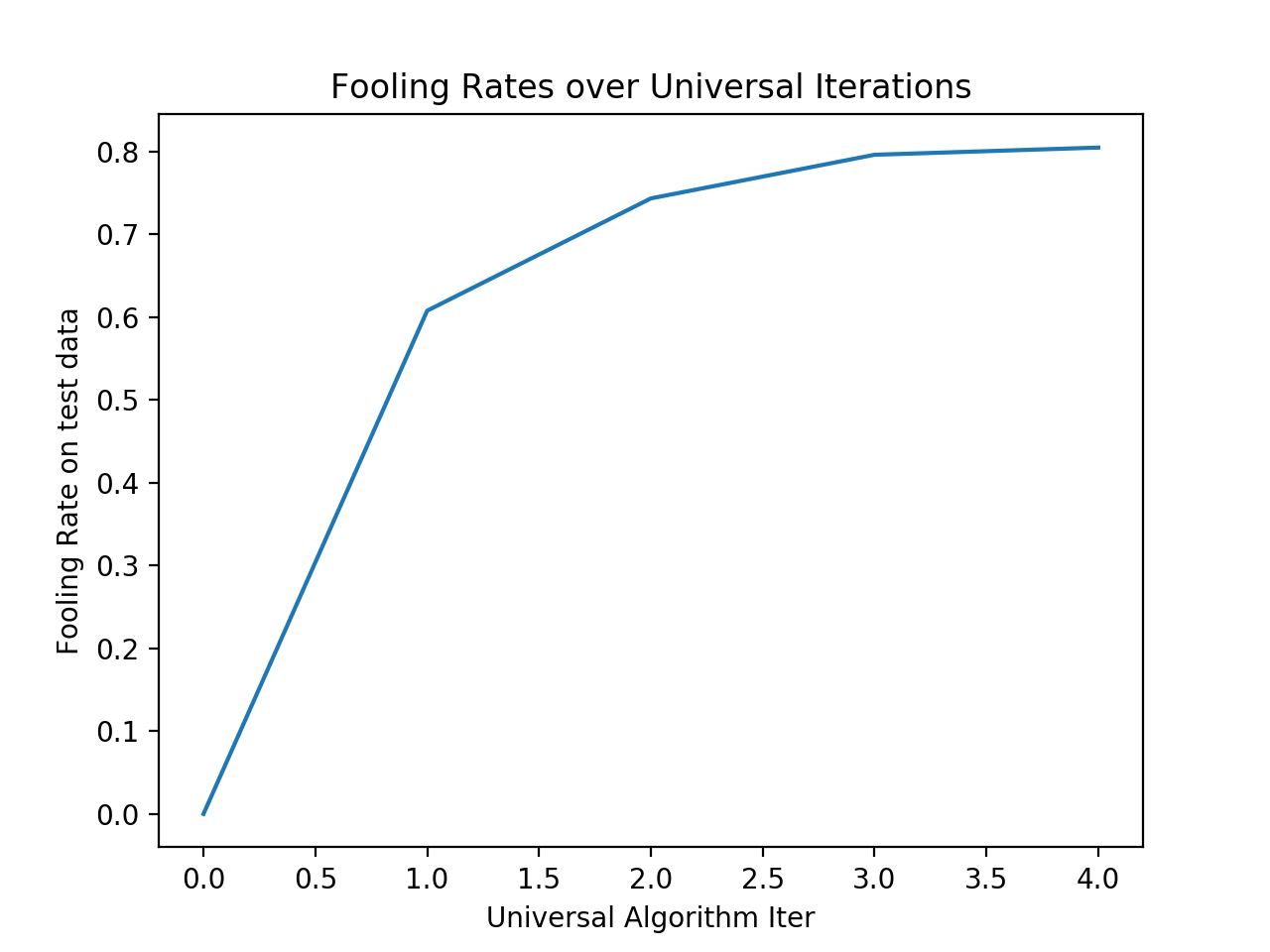
Fooling rate
Evolution of the fooling rate per iteration of the universal adversarial perturbation algorithm , using only 100 images from the train data to generate universal perturbations.
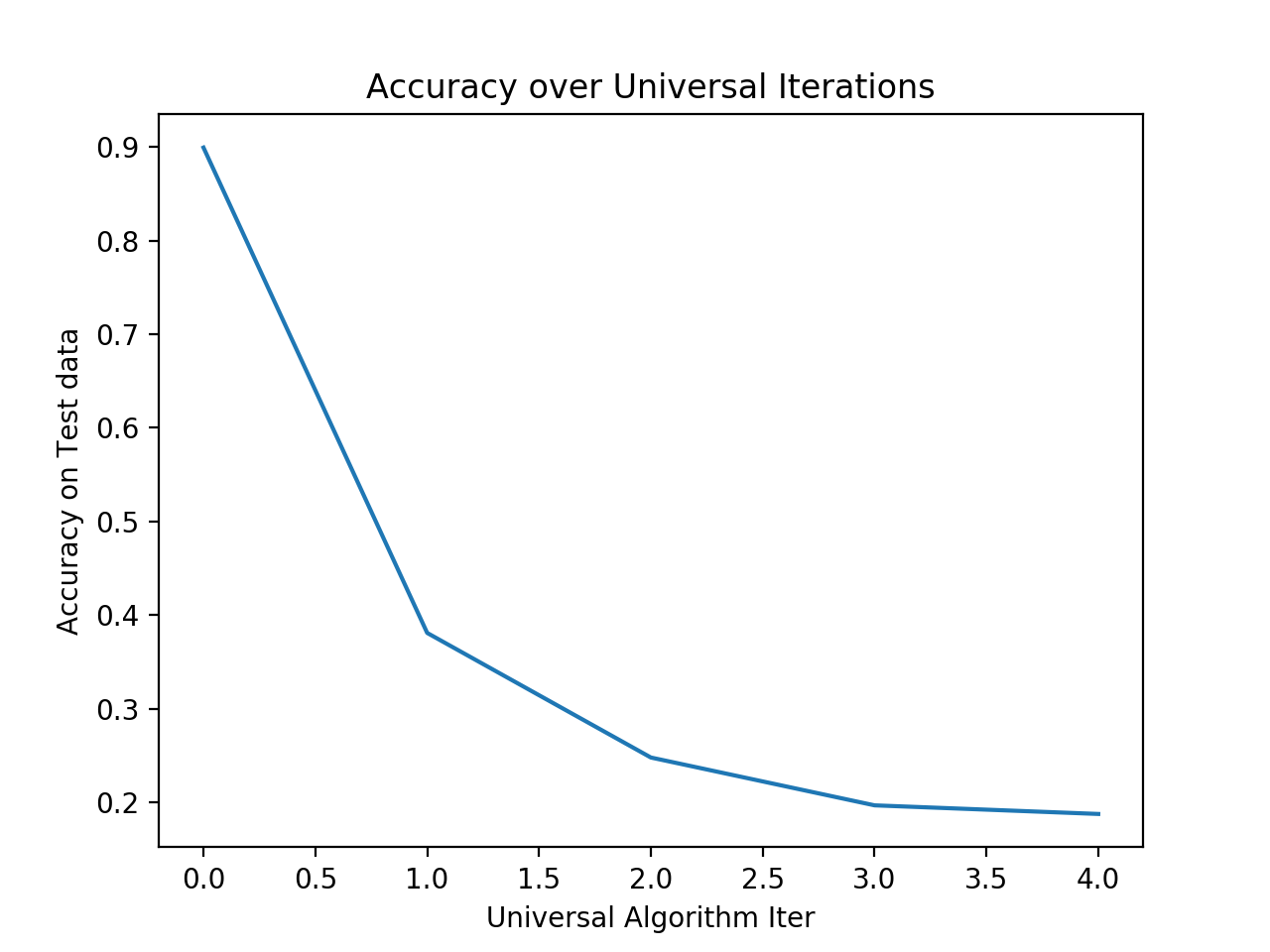
Accuracy
Evolution of the accuracy of the network on the test set when added the final perturbation of some iteration.